Getting Started with the ipd Package • ipd

Introduction

Background

With the rapid advancement of artificial intelligence and machine learning (AI/ML), researchers from a wide range of disciplines increasingly use predictions from pre-trained algorithms as outcome variables in statistical analyses. However, reifying algorithmically-derived values as measured outcomes may lead to biased estimates and anti-conservative inference (Hoffman et al., 2023). The statistical challenges encountered when drawing inference on predicted data (IPD) include:

Understanding the relationship between predicted outcomes and their true, unobserved counterparts
Quantifying the robustness of the AI/ML models to resampling or uncertainty about the training data
Appropriately propagating both bias and uncertainty from predictions into downstream inferential tasks

Several works have proposed methods for IPD, including post-prediction inference (PostPI) by Wang et al., 2020, prediction-powered inference (PPI) and PPI++ by Angelopoulos et al., 2023a and Angelopoulos et al., 2023b, and post-prediction adaptive inference (PSPA) by Miao et al., 2023. To enable researchers and practitioners interested in these state-of-the-art methods, we have developed ipd, a open-source R package that implements these methods under the umbrella of IPD.

This vignette provides a guide to using the ipd package, including installation instructions, examples of data generation, model fitting, and usage of custom methods. The examples demonstrate the package’s functionality.

Notation

Following the notation of Miao et al., 2023, we assume we have the following data structure:

We have two datasets: a labeled dataset, $\mathcal{L} = \left\{Y^\mathcal{L}, X^\mathcal{L}, f\left(X^\mathcal{L}\right)\right\}$ , and an unlabeled dataset, $\left\{X^\mathcal{U}, f\left(X^\mathcal{U}\right)\right\}$ . The labeled set is typically smaller in size compared to the unlabeled set.
We have access to an algorithm $f(X)$ that can predict our outcome of interest $Y$ .
Our interest is in performing inference on a quantity such as the outcome mean or quantile, or to recover a downstream inferential (mean) model:

$\mathbb{E}\left[Y^{\mathcal{U}} \mid \boldsymbol{X}^{\mathcal{U}}\right] = g^{-1}\left(\boldsymbol{X}^{\mathcal{U}'}\beta\right),$

where $\beta$ is a vector of regression coefficients and $g(\cdot)$ is a given link function, such as the identity link for linear regression, the logistic link for logistic regression, or the log link for Poisson regression. However, in practice, we do not observe $Y^\mathcal{U}$ in the ‘unlabeled’ subset of the data. Instead, these values are replaced by the predicted $f(X^\mathcal{U})$ . We can use methods for IPD to obtain corrected estimates and standard errors when we replace these unobserved $Y^\mathcal{U}$ by $f(X^\mathcal{U})$ .

Installation

To install the development version of ipd from GitHub, you can use the devtools package:

#-- Install devtools if it is not already installed

install.packages("devtools")   

#-- Install the ipd package from GitHub

devtools::install_github("ipd-tools/ipd")

Usage

We provide a simple example to demonstrate the basic use of the functions included in the ipd package.

#-- Load ipd Package

library(ipd)

Data Generation

The ipd packages provides a unified function, simdat, for generating synthetic datasets for various models. The function currently supports “mean”, “quantile”, “ols”, “logistic”, and “poisson” models.

Function Arguments

n: A vector of size 3 indicating the sample size in the training, labeled, and unlabeled data sets.
effect: A float specifying the regression coefficient for the first variable of interest (defaults to 1).
sigma_Y: A float specifying the residual variance for the generated outcome.
model: The type of model to be generated. Must be one of "mean", "quantile", "ols", "logistic", or "poisson".

The simdat function generate a data.frame with three subsets: (1) an independent “training” set with additional observations used to fit a prediction model, and “labeled” and “unlabeled” sets which contain the observed and predicted outcomes and the simulated features of interest.

Generating Data for Linear Regression

We can generate a continuous outcome and relevant predictors for linear regression as follows. The simdat function generates four independent covariates, $X_1$ , $X_2$ , $X_3$ , and $X_4$ , and the outcome:

$Y = \text{effect}\times X_1 + \frac{1}{2}\times X_2^2 + \frac{1}{3}\times X_3^3 + \frac{1}{4}\times X_4^2 + \varepsilon_y$

where effect is one of the function arguments and $\varepsilon_y \sim N(0, \text{sigma_Y})$ , with sigma_Y being another argument. Here, the simdat function generates three subsets of data, a “training” subset, a “labeled” subset, and an “unlabeled” subset, based on the sizes in n. It then learns the prediction rule for the outcome in the “training” subset using a generalized additive model and predicts these outcomes in the “labeled” and “unlabeled” subsets:

#-- Generate a Dataset for Linear Regression

set.seed(123)

n <- c(10000, 500, 1000)

dat_ols <- simdat(n = n, effect = 1, sigma_Y = 4, model = "ols")

#-- Print First 6 Rows of Training, Labeled, and Unlabeled Subsets

options(digits=2)

head(dat_ols[dat_ols$set == "training",])
#>       X1    X2    X3     X4     Y  f      set
#> 1 -0.560 -0.56  0.82 -0.356 -0.15 NA training
#> 2 -0.230  0.13 -1.54  0.040 -4.49 NA training
#> 3  1.559  1.82 -0.59  1.152 -1.08 NA training
#> 4  0.071  0.16 -0.18  1.485 -3.67 NA training
#> 5  0.129 -0.72 -0.71  0.634  2.19 NA training
#> 6  1.715  0.58 -0.54 -0.037 -1.42 NA training

head(dat_ols[dat_ols$set == "labeled",])
#>          X1      X2    X3    X4     Y     f     set
#> 10001  2.37 -1.8984  0.20 -0.17  1.40  3.24 labeled
#> 10002 -0.17  1.7428  0.26 -2.05  3.56  1.03 labeled
#> 10003  0.93 -1.0947  0.76  1.25 -3.66  2.37 labeled
#> 10004 -0.57  0.1757  0.32  0.65 -0.56  0.58 labeled
#> 10005  0.23  2.0620 -1.35  1.46 -0.82 -0.15 labeled
#> 10006  1.13 -0.0028  0.23 -0.24  7.30  2.16 labeled

head(dat_ols[dat_ols$set == "unlabeled",])
#>          X1     X2    X3    X4    Y     f       set
#> 10501  0.99 -3.280 -0.39  0.97  8.4  1.25 unlabeled
#> 10502 -0.66  0.142 -1.36 -0.22 -7.2 -1.08 unlabeled
#> 10503  0.58 -1.368 -1.73  0.15  5.6 -0.31 unlabeled
#> 10504 -0.14 -0.728  0.26 -0.23 -4.2  0.91 unlabeled
#> 10505 -0.17 -0.068 -1.10  0.58  2.2 -0.39 unlabeled
#> 10506  0.58  0.514 -0.69  0.97 -1.2  0.76 unlabeled

The simdat function provides observed and unobserved outcomes for both the labeled and unlabeled datasets, though in practice the observed outcomes are not in the unlabeled set. We can visualize the relationships between these variables in the labeled data subset:

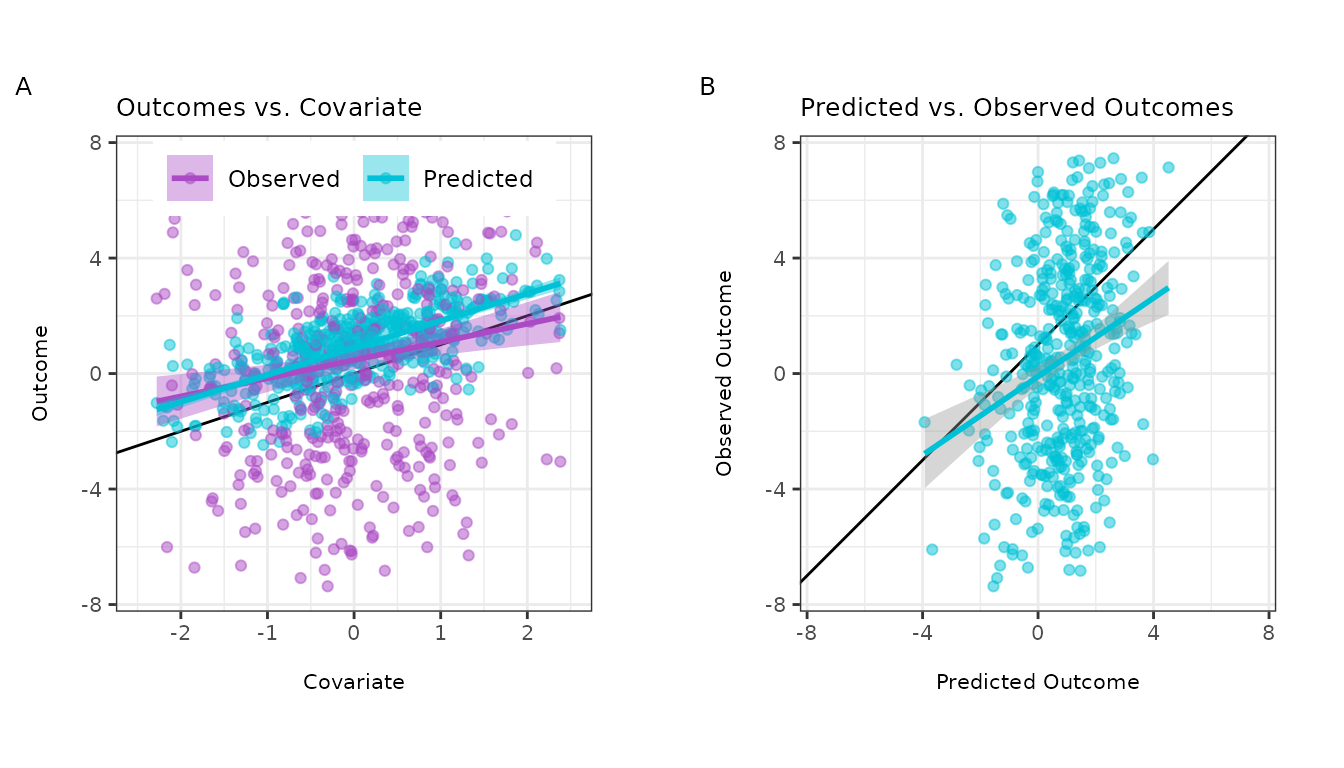
We can see that:

The predicted outcomes are more correlated with the covariate than the true outcomes (plot A)
The predicted outcomes are not perfect substitutes for the true outcomes (plot B)

Generating Data for Logistic Regression

As another example, we can generate a binary outcome and relevant predictors for logistic regression as follows:

#-- Generate a Dataset for Logistic Regression

set.seed(123)

dat_logistic <- simdat(n = n, effect = 3, sigma_Y = 1, 
                       
  model = "logistic")

#-- Print First 6 Rows of Training, Labeled, and Unlabeled Subsets

head(dat_logistic[dat_logistic$set == "training",])
#>       X1    X2    X3     X4 Y  f      set
#> 1 -0.560 -0.56  0.82 -0.356 1 NA training
#> 2 -0.230  0.13 -1.54  0.040 0 NA training
#> 3  1.559  1.82 -0.59  1.152 1 NA training
#> 4  0.071  0.16 -0.18  1.485 0 NA training
#> 5  0.129 -0.72 -0.71  0.634 0 NA training
#> 6  1.715  0.58 -0.54 -0.037 1 NA training

head(dat_logistic[dat_logistic$set == "labeled",])
#>          X1      X2    X3    X4 Y f     set
#> 10001  2.37 -1.8984  0.20 -0.17 1 1 labeled
#> 10002 -0.17  1.7428  0.26 -2.05 1 1 labeled
#> 10003  0.93 -1.0947  0.76  1.25 1 1 labeled
#> 10004 -0.57  0.1757  0.32  0.65 1 0 labeled
#> 10005  0.23  2.0620 -1.35  1.46 1 1 labeled
#> 10006  1.13 -0.0028  0.23 -0.24 1 1 labeled

head(dat_logistic[dat_logistic$set == "unlabeled",])
#>          X1     X2    X3    X4 Y f       set
#> 10501  0.99 -3.280 -0.39  0.97 1 1 unlabeled
#> 10502 -0.66  0.142 -1.36 -0.22 0 0 unlabeled
#> 10503  0.58 -1.368 -1.73  0.15 1 1 unlabeled
#> 10504 -0.14 -0.728  0.26 -0.23 0 0 unlabeled
#> 10505 -0.17 -0.068 -1.10  0.58 1 0 unlabeled
#> 10506  0.58  0.514 -0.69  0.97 1 1 unlabeled

We can again visualize the relationships between the true and predicted outcome variables in the labeled data subset and see that 81.8% observations are correctly predicted:

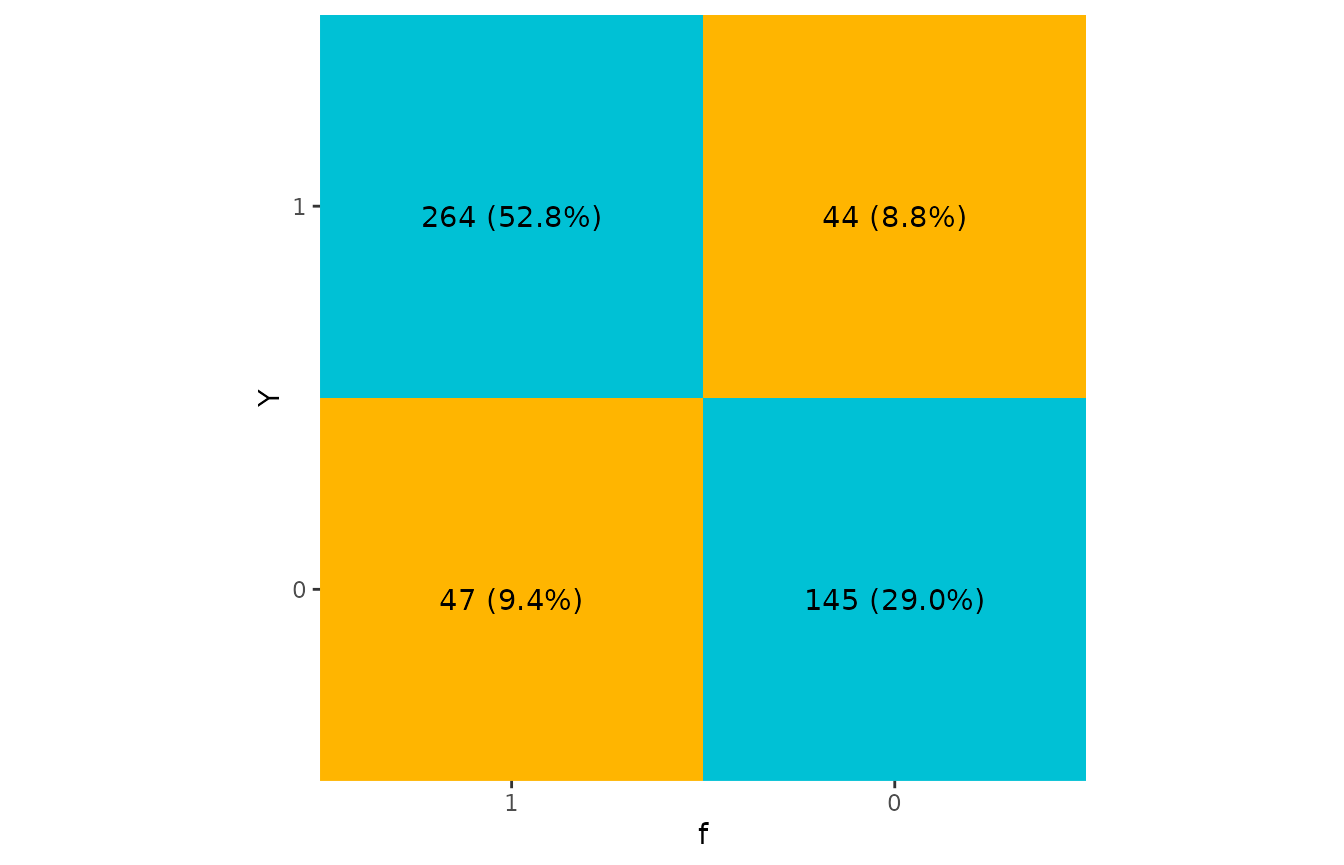
Model Fitting

Linear Regression

We compare two non-IPD approaches to analyzing the data to methods included in the ipd package.

0.1 ‘Naive’ Regression Using the Predicted Outcomes

#--- Fit the Naive Regression

lm(f ~ X1, data = dat_ols[dat_ols$set == "unlabeled",]) |> 
  
  summary()
#> 
#> Call:
#> lm(formula = f ~ X1, data = dat_ols[dat_ols$set == "unlabeled", 
#>     ])
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -2.5426 -0.6138 -0.0153  0.6345  2.8907 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   0.8391     0.0297    28.3   <2e-16 ***
#> X1            0.9848     0.0296    33.3   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.94 on 998 degrees of freedom
#> Multiple R-squared:  0.527,  Adjusted R-squared:  0.526 
#> F-statistic: 1.11e+03 on 1 and 998 DF,  p-value: <2e-16

0.2 ‘Classic’ Regression Using only the Labeled Data

#--- Fit the Classic Regression

lm(Y ~ X1, data = dat_ols[dat_ols$set == "labeled",]) |> 
  
  summary()
#> 
#> Call:
#> lm(formula = Y ~ X1, data = dat_ols[dat_ols$set == "labeled", 
#>     ])
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -15.262  -2.828  -0.094   2.821  11.685 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)    0.908      0.187    4.86  1.6e-06 ***
#> X1             1.097      0.192    5.71  1.9e-08 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 4.2 on 498 degrees of freedom
#> Multiple R-squared:  0.0614, Adjusted R-squared:  0.0596 
#> F-statistic: 32.6 on 1 and 498 DF,  p-value: 1.95e-08

You can fit the various IPD methods to your data and obtain summaries using the provided wrapper function, ipd():

1.1 PostPI Bootstrap Correction (Wang et al., 2020)

#-- Specify the Formula

formula <- Y - f ~ X1

#-- Fit the PostPI Bootstrap Correction

nboot <- 200

ipd::ipd(formula, 
         
  method = "postpi_boot", model = "ols", data = dat_ols, label = "set", 
  
  nboot = nboot) |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: postpi_boot 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.873     0.183    0.514     1.23
#> X1             1.151     0.183    0.793     1.51

1.2 PostPI Analytic Correction (Wang et al., 2020)

#-- Fit the PostPI Analytic Correction

ipd::ipd(formula, 
         
  method = "postpi_analytic", model = "ols", data = dat_ols, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: postpi_analytic 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.865     0.183    0.505     1.22
#> X1             1.145     0.182    0.788     1.50

2. Prediction-Powered Inference (PPI; Angelopoulos et al., 2023)

#-- Fit the PPI Correction

ipd::ipd(formula, 
         
  method = "ppi", model = "ols", data = dat_ols, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: ppi 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.871     0.182    0.514     1.23
#> X1             1.122     0.195    0.740     1.50

3. PPI++ (Angelopoulos et al., 2023)

#-- Fit the PPI++ Correction

ipd::ipd(formula, 
         
  method = "ppi_plusplus", model = "ols", data = dat_ols, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: ppi_plusplus 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.881     0.182    0.524     1.24
#> X1             1.116     0.187    0.750     1.48

4. post-prediction adaptive inference (PSPA; Miao et al., 2023)

#-- Fit the PSPA Correction

ipd::ipd(formula, 
         
  method = "pspa", model = "ols", data = dat_ols, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: pspa 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.881     0.182    0.524     1.24
#> X1             1.109     0.187    0.743     1.47

Logistic Regression

We also show how these methods compare for logistic regression.

0.1 ‘Naive’ Regression Using the Predicted Outcomes

#--- Fit the Naive Regression

glm(f ~ X1, family = binomial, 
    
  data = dat_logistic[dat_logistic$set == "unlabeled",]) |> 
  
  summary()
#> 
#> Call:
#> glm(formula = f ~ X1, family = binomial, data = dat_logistic[dat_logistic$set == 
#>     "unlabeled", ])
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)    1.173      0.125    9.36   <2e-16 ***
#> X1             3.832      0.257   14.93   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1328.13  on 999  degrees of freedom
#> Residual deviance:  569.36  on 998  degrees of freedom
#> AIC: 573.4
#> 
#> Number of Fisher Scoring iterations: 7

0.2 ‘Classic’ Regression Using only the Labeled Data

#--- Fit the Classic Regression

glm(Y ~ X1, family = binomial,
   
  data = dat_logistic[dat_logistic$set == "labeled",]) |> 
  
  summary()
#> 
#> Call:
#> glm(formula = Y ~ X1, family = binomial, data = dat_logistic[dat_logistic$set == 
#>     "labeled", ])
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)    0.677      0.121    5.58  2.5e-08 ***
#> X1             2.064      0.196   10.56  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 665.99  on 499  degrees of freedom
#> Residual deviance: 449.44  on 498  degrees of freedom
#> AIC: 453.4
#> 
#> Number of Fisher Scoring iterations: 5

You can again fit the various IPD methods to your data and obtain summaries using the provided wrapper function, ipd():

1. PostPI Bootstrap Correction (Wang et al., 2020)

#-- Specify the Formula

formula <- Y - f ~ X1

#-- Fit the PostPI Bootstrap Correction

nboot <- 200

ipd::ipd(formula, method = "postpi_boot", model = "logistic", 
         
  data = dat_logistic, label = "set", nboot = nboot) |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: postpi_boot 
#> Model: logistic 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)   0.5503    0.0741   0.4052      0.7
#> X1            1.1252    0.0891   0.9506      1.3

2. Prediction-Powered Inference (PPI; Angelopoulos et al., 2023)

#-- Fit the PPI Correction

ipd::ipd(formula, method = "ppi", model = "logistic", 
         
  data = dat_logistic, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: ppi 
#> Model: logistic 
#> Intercept: Yes 
#> 
#> Coefficients:
#>      Estimate Std.Error Lower.CI Upper.CI
#> [1,]    0.711     0.162    0.394     1.03
#> [2,]    2.092     0.214    1.673     2.51

3. PPI++ (Angelopoulos et al., 2023)

#-- Fit the PPI++ Correction

ipd::ipd(formula, method = "ppi_plusplus", model = "logistic", 
         
  data = dat_logistic, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: ppi_plusplus 
#> Model: logistic 
#> Intercept: Yes 
#> 
#> Coefficients:
#>      Estimate Std.Error Lower.CI Upper.CI
#> [1,]    0.688     0.128    0.438     0.94
#> [2,]    2.074     0.189    1.702     2.44

4. Post-Prediction Adaptive Inference (PSPA; Miao et al., 2023)

#-- Fit the PSPA Correction

ipd::ipd(formula, method = "pspa", model = "logistic", 
         
  data = dat_logistic, label = "set") |> 
  
  summary()
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: pspa 
#> Model: logistic 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.684     0.124    0.441     0.93
#> X1             2.072     0.192    1.695     2.45

Printing, Summarizing, and Tidying

The package also provides custom print, summary, tidy, glance, and augment methods to facilitate easy model inspection:

#-- Fit the PostPI Bootstrap Correction

nboot <- 200

fit_postpi <- ipd::ipd(formula, 
         
  method = "postpi_boot", model = "ols", data = dat_ols, label = "set", 
  
  nboot = nboot)

Print Method

The print method gives an abbreviated summary of the output from the ipd function:

#-- Print the Model

print(fit_postpi)
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Coefficients:
#> (Intercept)          X1 
#>        0.87        1.15

Summary Method

The summary method gives more detailed information about the estimated coefficients, standard errors, and confidence limits:

#-- Summarize the Model

summ_fit_postpi <- summary(fit_postpi)
  
#-- Print the Model Summary

print(summ_fit_postpi)
#> 
#> Call:
#>  Y - f ~ X1 
#> 
#> Method: postpi_boot 
#> Model: ols 
#> Intercept: Yes 
#> 
#> Coefficients:
#>             Estimate Std.Error Lower.CI Upper.CI
#> (Intercept)    0.867     0.183    0.508     1.23
#> X1             1.154     0.183    0.796     1.51

Tidy Method

The tidy method organizes the model coefficients into a tidy format.

#-- Tidy the Model Output

tidy(fit_postpi)
#>                    term estimate std.error conf.low conf.high
#> (Intercept) (Intercept)     0.87      0.18     0.51       1.2
#> X1                   X1     1.15      0.18     0.80       1.5

Glance Method

The glance method returns a one-row summary of the model fit.

#-- Get a One-Row Summary of the Model

glance(fit_postpi)
#>        method model include_intercept nobs_labeled nobs_unlabeled       call
#> 1 postpi_boot   ols              TRUE          500           1000 Y - f ~ X1

Augment Method

The augment method adds model predictions and residuals to the original dataset.

#-- Augment the Original Data with Fitted Values and Residuals

augmented_df <- augment(fit_postpi)

head(augmented_df)
#>          X1     X2    X3    X4    Y     f       set .fitted .resid
#> 10501  0.99 -3.280 -0.39  0.97  8.4  1.25 unlabeled    2.00    6.4
#> 10502 -0.66  0.142 -1.36 -0.22 -7.2 -1.08 unlabeled    0.10   -7.3
#> 10503  0.58 -1.368 -1.73  0.15  5.6 -0.31 unlabeled    1.53    4.1
#> 10504 -0.14 -0.728  0.26 -0.23 -4.2  0.91 unlabeled    0.71   -4.9
#> 10505 -0.17 -0.068 -1.10  0.58  2.2 -0.39 unlabeled    0.67    1.5
#> 10506  0.58  0.514 -0.69  0.97 -1.2  0.76 unlabeled    1.53   -2.7

Conclusions

The ipd package offers a suite of functions for conducting inference on predicted data. With custom methods for printing, summarizing, tidying, glancing, and augmenting model outputs, ipd streamlines the process of IPD-based inference in R. We will continue to develop this package to include more targets of inference and IPD methods as they are developed, as well as additional functionality for analyzing such data. For further information and detailed documentation, please refer to the function help pages within the package, e.g.,

?ipd

Feedback

For questions, comments, or any other feedback, please contact the developers (ssalerno@fredhutch.org).

Contributing

Contributions are welcome! Please open an issue or submit a pull request on GitHub.

License

This package is licensed under the MIT License.